Operações com Números Complexos
Dado o complexo z = a + bi, dizemos que a é a parte real de z indicada por Re(z) e b é a parte imaginária de z indicada por Im(z).
O número z = a + bi é chamado:
Número imaginário: quando b diferente de 0;
Número imaginário puro: quando b diferente de 0 e a = 0;
Número real: quando b = 0
Igualdade de Números Complexos
Dois números complexos, z1 = a + bi e z2 = c + di, são iguais se, e somente se, possuem as partes reais iguais entre si, a = c, e as partes imaginárias iguais entre si, b = d.

Exemplos
a) z = 5 – 2i
b) z = 7 + 4i
c) z = 8
d) z = 6i
Re(z) = 5 e Im(z) = -2
Re(z) = 7 e Im(z) = 4
Re(z) = 8 e Im(z) = 0
Re(z) = 0 e Im(z) = 6
Número Real
Imaginário Puro
Adição de Números Complexos
A soma de dois números complexos, z1 = a + bi e z2 = c + di, é o complexo z1 + z2 cuja parte real é igual a soma das partes reais de z1 e z2 e cuja parte imaginária é igual à soma das partes imaginárias de z1 e z2

Propriedades
1 – Associativa: (z1 + z2) + z3 = z1 + (z2 + z3)
2 – Comutativa: z1 + z2 = z2 + z1
3 – Elemento Neutro: z + 0 = 0 + z = 0
4 – Oposto: z = a + bi tem oposto igual – z = – a – bi tal que z + (- z) = 0
Exemplos
Dados z1 = 3 + 6i, z2 = -2 – 5i e z3 = 2i temos:
z1 + z2 = 1 + i
z1 + z3 = 3 + 8i
z2 + z3 = -2 – 3i
Subtração de Números Complexos
A subtração de dois números complexos, z1 = a + bi e z2 = c + di, é o complexo z1 – z2 cujo resultado da parte real é a soma parte real de z1 com o oposto da parte real de z2 e cujo resultado da parte imaginária é a soma da parte imaginária de z1 com o oposto da parte imaginária de z2.

Para a subtração valem as mesmas propriedades operatória da adição que foram apresentadas.
Exemplos
Dados z1 = 1 + 2i, z2 = -3 -i e z3 = 5i, temos:
z1 – z2 = (1 + 2i) – ( -3 -i ) = 1 + 2i + 3 + 1 = 4 + 3i
z1 + z2 – z3 = (1 + 2i) + ( -3 -i ) – 5i = 1 + 2i -3 – i – 5i = -2 – 4i
Multiplicação de Números Complexos
O produto dos números complexos z1 = a + bi e z2 = c + di, é o complexo z1 . z2 cuja parte real é o produto das partes reais menos o produto das partes imaginárias, e cuja parte imaginária é a soma dos produtos da parte real de um deles pela parte imaginária do outro.
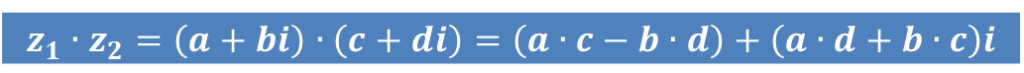
Propriedades
A multiplicação de números complexos goza das propriedades:
1 – Associativa: ( z1 . z2 ) . z3 = z1 . ( z2 . z3 )
2 – Comutativa: z1 . z2 = z2 . z1
3 – Elemento Neutro: 1 = 1 + 0i é o elemento neutro, pois z . 1 = 1 . z = 1
4 – Inverso: 1/z, pois z . 1/z = 1 com z diferente de zero.
Exemplos
Dados: z1 = 3 + 2i e z2 = 5 – 4i temos:
z1 . z2 = (3 + 2i) . (5 – 4i) = 15 – 12i + 10i – 8i² = 15 – 12i + 10i -(-8) = 23 – 2i
Exercícios Resolvidos
Igualdade de Números Complexos
Dados os números complexos z1 = (x, 3) e z2 = (2 – y, y), determine os números reais x e y de modo que z2 + z1 = (5, -4).
Igualdade de Números Complexos
Em cada caso, determine os números reais m e n para que a igualdade seja verdadeira.
a) m + (n + 1)i = -4 + 3i
b) (n – 2, m + 5) = (3, 2i)
c) (m – 3) + (n – 2)i = 5i
d) (m – n + 1) + (2m + n – 4)i = 0
Soma e Subtração de Números Complexos
Efetue:
a) (-7 + 5i) – (3 – 2i)
b) 2 + (3 – i) + (-1 + 2i) + i
c) (-4 + 3i) + 2i – (-3 – i)
d) -1 – (-2 + i) + (5 – i) – (3 – 7i)
