Exercício 1 – Usando a definição, calcule o valor dos seguintes logaritmos.

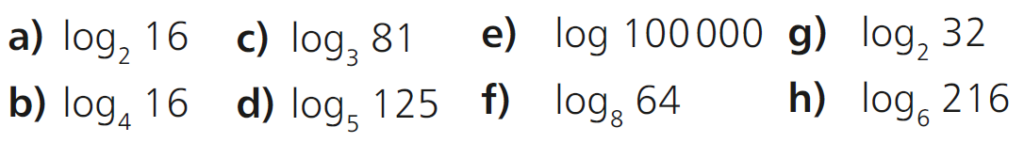
Exercício 2 – Use a definição para calcular.

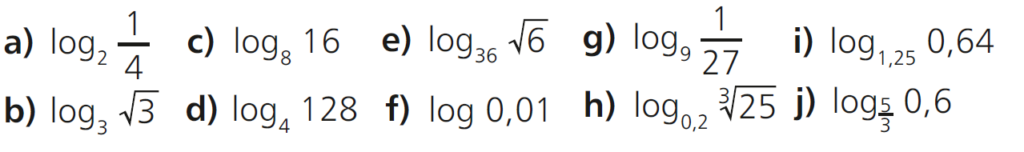
Exercício 3 – Coloque em ordem crescente os seguintes números reais.
A = log₂₅ 0,2
B = log₇ 1/49
C = log_0,25 8
D = log 0,1

Exercício 4 – Qual é o valor de cada uma das expressões seguintes?
a) log₅ 5 + log₃ 1 – log 10
b) log_1/4 4 + log₄ 1/4
c) log 1000 + log 100 + log 10 + log 1

Exercício 5 – Calcule o valor do Logaritmo.

Exercício 6 – Exercícios resolvidos de Logaritmos – Obtenha, em cada caso, o valor real de x:
a) log5 x = log5 16
b) log3 (4x – 1) = log3 x
c) log x^2 = log x
d) logx(2x – 3) = logx(- 4x + 8)

Exercício 7 – Função Logarítmica

Exercício 8 – Calcule o valor do logaritmo.

Exercício 9 – Determine o Valor de m na Equação
Determine m, com m E R, a fim de que a equação x² + 4x + log2 m = 0, na incógnita x, admita uma raiz real dupla.
Qual é essa raiz?

Exercício 10 – Calcule o valor da potência.

Exercício 11 – Calculo do logaritmo natural e decimal.

Exercício 12 – Calcule o valor dos seguintes Logaritmos
Sejam x, y, b reais positivos, b = 1. Sabendo que log x = -2 e log y = 3, calcule o valor dos seguintes logaritmos:
a) log (x*y)
b) log (x/y)
c) log (x³ * y²)
d) log (y² / Vx)

Exercício 13 – Propriedades Operatórias dos Logaritmos
Desenvolva, aplicando as propriedades operatórias dos logaritmos (suponha a, b, e c reais positivos):
a) log 5 (5a/bc)
b) log (b²/10a)
c) log 3 (ab²/c)
d) log 2 (8a/b³c²)
e) log 2 V(8a²b³)

Exercício 14 – Calcule o logaritmo em função de a e b.
Sabendo que log 2 = a e log 3 = b, calcule, em função de a e b: a) log 6
b) log 1,5
c) log 5
d) log 30
e) log 1/4
f) log 72
g) log 0,3
h) log V1,8
i) log 0,024
j) log 0,75
k) log 20000

Exercício 15 – Propriedades Operatórias dos Logaritmos
Sejam a, b e c reais positivos. Em cada caso, obtenha a expressão cujo desenvolvimento logarítmico, na respectiva base, é dado por:
a) log a + log b + log c
b) 3 log2 a + 2 log2 c – log2 b
c) log3 a – log3 b – 2
d) 1/2 log – 2 log b

Exercício 16 – Calcule o valor do Logaritmo por meio das propriedades operatórias.

Exercício 17 – Calcule o valor de x utilizando as propriedades operatórias.

Exercício 18 – Calcule o valor do Logaritmo.

Exercício 19 – Obtenha os Valores dos Logaritmos
Considerando que log₂ 5 = 2,32, obtenha os valores de:
a) log₂ 10
b) log₂ 500
c) log₂ 1600

Exercício 20 – Classifique em Verdadeiro ou Falso
Classifique as afirmações seguintes em verdadeiras (V) ou falsas (F):
a) log 26 = log 20 + log 6
b) log 5 + log 8 + log 2,5 = 2
c) log2 418 = 36
d) log3 3 . 0,25

Exercício 21 – Percentual da Informação
(UFPR) Para determinar a rapidez com que se esquece de uma informação, foi efetuado um teste em que listas de palavras eram lidas a um grupo de pessoas e, num momento posterior, verificava-se quantas dessas palavras eram lembradas. Uma análise mostrou que, de maneira aproximada, o percentual S de palavras lembradas, em função do tempo t, em minutos, após o teste ter sido aplicado, era dado pela expressão: S = -18 * log (t + 1) + 86
a) Após 9 minutos, que percentual da informação inicial era lembrado?
b) Depois de quanto tempo o percentual S alcançou 50%?

Exercício 22 – Equação com Logaritmos
Resolva, em R, as seguintes equações:
a) 2 log (x + 3) = log (x² + 45)
b) log (4x – 1) – log (x + 2) = log x
c) 3 log 2 + log (x – 1) = 0
d) 2 log x = log (2x – 3) + log (x +2)
e) log x + log x² + log x³ = – 6

Exercício 23 – Sistema de Equações com Logaritmos
Resolva, em R, os seguintes sistemas de equações:
a) x + y = 10
log4 x + log4 y = 2
b) 4x – y = 8
log2 x – log2 y = 2

Exercício 24 – Escreva na base 2 os seguintes logaritmos.

Exercício 25 – Calcule o valor dos logaritmos.

Exercício 26 – Calcule o valor do logaritmo.

Exercício 27 – Sabendo que log12 5 = a, calcule, em função de a, o valor dos seguintes logaritmos:
a) log5 12
b) log25 12
c) log5 60
d) log125 144

Exercício 28 – Qual é o valor de:

Exercício 29 – Estabeleça o Domínio de Função Logarítmica
Estabeleça o domínio de cada uma das funções logarítmicas seguintes, definidas por:
a) y = log (x – 1)
b) y = log (3x – 2)
c) y = log (x² – 9)
d) y = log (x² + 3)

Exercício 30 – Classifique como Verdadeiras ou Falsas
Seja f: R* em R definida por f(x) = log x. Classifique como verdadeira (V) ou falsa (F) as afirmações seguintes, corrigindo as falsas:
a) f(100) = 2
b) f(x2) = 2 * f(x)

Exercício 31 – Construa o Gráfico das Funções Logarítmicas
Construa o gráfico das funções logarítmicas de domínio R+ definidas pelas leis seguintes:
a) y = log x

Exercício 32 – Domínio da Função Logarítmica
O gráfico abaixo representa a função definida pela lei y = a + log (x + 1), sendo a e b constantes reais.
a) Qual é o domínio de f?
b) Quais são os valores de a e b, respectivamente?

Exercício 33 – Área do Retângulo ABCD
O gráfico abaixo representa a função f, definida por f(x) = log (x + k), sendo k uma constante real.
a) Qual é o valor de k?
b) Qual é a área do retângulo ABCD?
c) Qual é o valor de f(1001)?

Exercício 34 – Sinal do Logaritmos
Entre os números seguintes, determine aqueles que são positivos: a) log1/4 3
b) log5 2
c) log 0,2
d) log1/2 1/3
e) log2/3 7
f) ln 2

Exercício 35 – Estimativa de Funcionários de uma Empresa
A lei seguinte representa uma estimativa sobre o número de funcionários de uma empresa, em função do tempo t, em anos (t = 0, 1, 2, …), de existência da empresa: f(t) = 400 + 50 log4 (t + 2)
a) Quantos funcionários a empresa possuía na sua fundação?
b) Quantos funcionários foram incorporados à empresa do 2º ao 6º ano? (Admita que nenhum funcionário tenha saído.)
c) Calcule a taxa média de variação do número de funcionários da empresa do 6º ao 14º ano.

Exercício 36 – Área do Triângulo ABC
O gráfico da função f: R em R, definida por y = ln x, é dado a seguir: Determine a área do triângulo ABC, usando a tabela seguinte, que contém valores aproximados.

Exercício 37 – Lei da Função e Valor de f(3) – g(3)
Os gráficos de duas funções f e g são mostrados a seguir:
Sabendo que f(x) = log x, determine:
a) a lei da função g
b) os valores reais de x para os quais f(x) maior que g(x)
c) o valor de f(3) – g(3)

Exercício 38 – Qual dos Números Reais é Maior?
Em cada item, decida qual dos números reais é maior:
a) log 4 e log 5
b) log pi e log 9
c) log V2 e log 2

Exercício 39 – Resolva as Seguintes Equações Exponenciais
Considerando log 2 = 0,3 e log 3 = 0,48, resolva as seguintes equações exponenciais:
a) 3x = 10
b) 4 exp{x} = 3
c) 2 exp{x} = 27

Exercício 40 – Dívida Externa de um País
Economistas afirmam que a dívida externa de um determinado país crescerá segundo a lei: y = 40 * 1,2x sendo y o valor da dívida (em bilhões de dólares) e x o número de anos transcorridos após a divulgação dessa previsão.
Em quanto tempo a dívida estará estimada em 90 bilhões de dólares?

Exercício 41 – Rendimento de Caderneta de Poupança
O investimento financeiro mais conhecido do brasileiro é a caderneta de poupança, que rende aproximadamente 6% ao ano. Ao aplicar hoje R$ 2000,00, um poupador terá, daqui a n anos, um valor v, em reais, dado por v(n) = 2 000 * 1,06n.
a) Que valor terá o poupador daqui a 3 anos? E daqui a 6 anos? Use 1,063 = 1,2.
b) Qual é o tempo mínimo (em anos inteiros) necessário para que o valor dessa poupança seja de R$ 4000,00? E R$ 6500,00?

Exercício 42 – Desvalorização de um Imóvel
Dentro de t décadas, contadas a partir de hoje, o valor (em reais) de um imóvel será estimado por v(t) = 600000 * 0,9t.
a) Qual é o valor atual desse imóvel?
b) Qual é a perda (em reais) no valor desse imóvel durante a primeira década?
c) Qual é a desvalorização percentual desse imóvel em uma década?
d) Qual é o tempo mínimo necessário, em anos, para que o valor do imóvel seja de 450 mil reais?

Exercício 43 – Tempo Aproximado de Uso de Equipamento
Um equipamento industrial foi adquirido por R$ 30000,00. Seu valor (v), em reais, com x anos de uso, é dado pela lei v(x) = pq em que p e q são constantes reais. Sabendo que, com 3 anos de uso, o valor do equipamento será R$ 21870,00, determine:
a) os valores de p e q
b) o tempo aproximado de uso para o qual o equipamento valerá R$ 10000,00

Exercício 44 – Crescimento de População em Anos
A população de certa espécie de mamífero em uma região da Amazônia cresce segundo a lei n(t) = 5000 e² em que n(t) é o número de elementos estimado da espécie no ano t (t =0, 1, 2, …), contado a partir de hoje (t = 0). Determine o número inteiro mínimo de anos necessários para que a população atinja:
a) 8000 elementos
b) 10000 elementos

Exercício 45 – Tempo de Decaimento Radioativo do Estrôncio
(Unicamp-SP) O decaimento radioativo do estrôncio 90 é descrito pela função P(t) = P0 2–bt, onde t é um instante de tempo, medido em anos, b é uma constante real e P0 é a concentração inicial do estrôncio 90, ou seja, a concentração no instante t = 0.
a) Se a concentração de estrôncio 90 cai pela metade em 29 anos, isto é, se a meia-vida do estrôncio 90 é de 29 anos, determine o valor constante de b.
b) Dada uma concentração inicial P0 de estrôncio 90, determine o tempo necessário para que a concentração seja reduzida a 20% de P0

Exercício 46 – Crescimento da População de Ratos
Estima-se que a população de ratos em um município cresça à taxa de 10% ao mês: isto é, a cada mês, o número de ratos aumentou 10% em relação ao número de ratos do mês anterior. Sabendo que a quantidade atual de ratos é da ordem de 400 000, determine o tempo mínimo de meses necessários para que a população de ratos nesse município quadruplique.

Exercício 47 – Tempo de Vida do Césio-137
Em setembro de 1987, Goiânia foi palco do maior acidente radioativo ocorrido no Brasil, quando uma amostra de césio-137, removida de um aparelho de radioterapia abandonado, foi manipulada inadvertidamente por parte da população. A meia-vida de um material radioativo é o tempo necessário para que a massa desse material se reduza à metade. A meia-vida do césio-137 é 30 anos e a quantidade restante de massa de um material radioativo, após t anos, é calculada pela expressão M(t) = A · (2,7)kt, onde A é a massa inicial e k é uma constante negativa.
Qual o tempo necessário, em anos, para que uma quantidade de massa do césio-137 se reduza a 10% da quantidade inicial?