Combinação Simples

Introdução

Em permutações, estamos interessados no número de maneiras de como ordenar os elementos de um conjunto de objetos. Em muitos problemas de contagem, a ordem dos elementos não é importante. Por exemplo, em um jogo de baralho, as cartas que estão nas mãos de algum jogador são sempre as mesmas independente de como ela estão dispostas. Logo, nosso interesse é saber o número de possíveis mãos de cinco cartas de 52 cartas existentes no baralho do que a ordem que elas aparecem nas mãos do jogador. Podemos desenvolver a fórmula para contar situações como citada acima.

A combinação de k elementos de um conjunto é qualquer subconjunto de n elementos do conjunto. Se o conjunto tem n elementos, então o número de combinações de k elementos é definido por C(n, k) e é chamado de o número de combinações de n elementos tomados de k a k vezes.

Por exemplo, considere um conjunto com quatro elementos, 1, 2, 3 e 4. A combinação desses quatro elementos tomados três a três vezes são:

A permutação desses elementos tomados três a três são:

Observe que o número de combinações (4) é muito menor que o número de permutações (24). Ou seja, estamos dividindo o número de permutações (24) pelo fatorial do agrupamento de 3 elementos (3! = 6).
Desse modo, podemos escrever a fórmula da combinação simples.

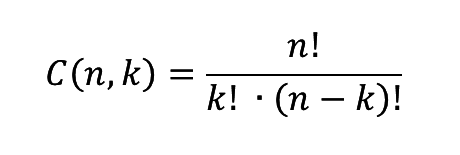
Exemplo

Um clube tem nove membros. De quantos modos diferentes pode ser criada uma comissão composta por três membros dentre os nove membros deste clube?
Solução: Como ser trata de uma comissão, a ordem de escolha dos membros não tem importância. Aplicando a fórmula de combinação simples teremos o resultado apresentado abaixo:

---

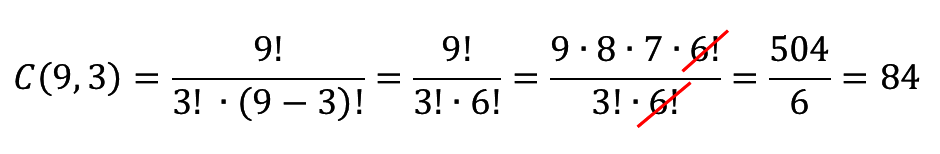
Exercícios Resolvidos