Definição
Em muitas das situações estudadas em Análise Combinatória aparecem, nos cálculos, o produto de números naturais consecutivos, tais como:
10 . 9 . 8 . 7 . 6 . 5 . 4 . 3 . 2 . 1 = 3628800
ou
7 . 6 . 5 . 4 . 3 . 2 . 1 = 5040
Sendo muito comum nos cálculos combinatórios expressões do tipo citado, torna-se conveniente adotar uma notação que simplifique sua representação. Essa notação é denominada notação fatorial.
Definimos fatorial de um número natural n, n maior ou igual a 2, como sendo o produto de todos os números naturais de n até 1. Representado pela notação n!

Também é definido o fatorial para n = 0 e n = 1:
0! = 1 e 1! = 1
Exemplos:
a) 4! = 4 . 3 . 2 . 1 = 24
b) 5! = 5 . 4 . 3 . 2 . 1 = 120
c) 6 . 5 . 4 . 3 . 2 . 1 = 6!
d) 7 . 6 . 5 . 4 . 3 . 2 . 1 = 7!
Quando necessário, podemos interromper a expansão de um fatorial antes de se atingir o número 1. Para tanto, basta colocar o símbolo de fatorial no algarismo escrito por último.
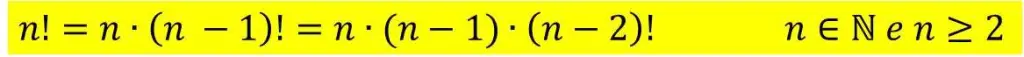
Exemplos:
a) 10! = 10 . 9!
b) 15! = 15 . 14 . 13 . 12 . 11!
c) (n + 2)! = (n + 2) . (n + 1) . n!
Exercícios Resolvidos
Calcule o fatorial.
a) 6!
b) 4!
c) 0! + 1!
d) 3! – 2!
e) 7! – 5!
f) 5 * 3!
Obtenha o valor de cada uma das expressões seguintes:
a) 8! / 6!
b) 9! / 10!
c) 3! / 4! + 4! / 5!
d) 7! / 5! * 2!
Efetue:
a) 11! + 9! / 10!
b) 17! – 17 * 16!
c) 40! – 39! / 41!
Simplifique:
a) (n + 2)! / (n + 1)!
b) (n – 3)! / (n – 2)!
Classifique como verdadeira (V) ou falsa (F) as seguintes afirmações, considerando que a e b são números naturais quaisquer.
a) (a + b)! = a! + b!
b) (a – b)! = a! – b!
c) (2a)! = 2 * a!
d) (a!)² = a! * a!
e) (a * b)! = a! * b!
