Formas de Representação
Analisando livros didáticos observa-se que diferentes autores adotam formas distintas de conceituar os números complexos. Alguns adotam a forma algébrica, outros adotam a forma cartesiana. Nesta página serão detalhadas as três formas de representação dos números complexos.
Forma Cartesiana
Na forma cartesiana utiliza-se o par ordenado (x, y), x e y números reais, para representar um número complexo. Sendo a abscissa x, a parte real e a ordenada y, a parte imaginária.
Nesse sentido são exemplos de números complexos: z1 = (-2, 3), z2 = (0, -1) e z3 = (3, 0). Valendo as seguintes propriedades operatórias:

Exemplo:
Se z1 = (2, 3) e z2 = (4, 5) então z1 + z2 = (6, 8) e z1 . z2 = (-7, 22)
Forma Algébrica
Esta é a forma mais utilizada para representar um número complexo que torna mais prática e simples as operações matemáticas. Indicando o número complexo pela letra z temos:
z = a + bi (a e b reais e i2 = -1)
a denomina-se parte real de z: a = Re(z);
b denomina-se parte imaginária de z: b = Im(z).
Chama-se número real a todo número complexo z tal que Im(z) = 0;
Chama-se número imaginário a todo número complexo z tal que Im(z) <> 0;
Chama-se número imaginário puro a todo número complexo z tal que Re(Z) = 0.
Valendo as seguintes propriedades operatórias:
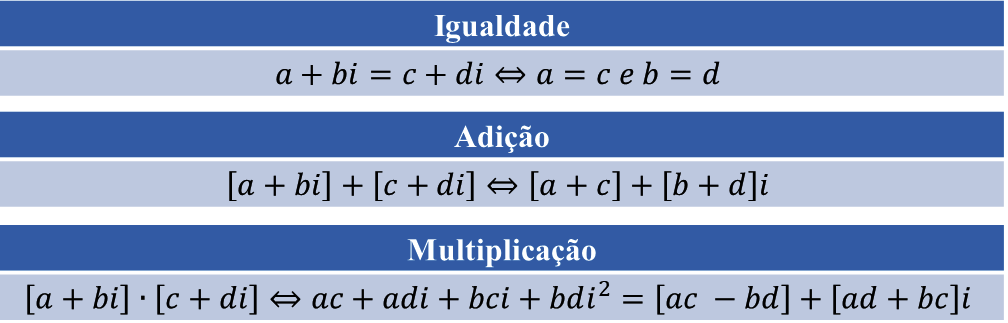
Exemplo:
a) z = 2 – 3i
b) z = 5
c) z = 4i
Re(z) = 2 e Im(z) = – 3
Re(z) = 5 e Im(z) = 0
Re(z) = 0 e Im(z) = 4
Forma Trigonométrica
Para representar na forma trigonométrica faremos uso da representação geométrica de um número complexo a partir de dois eixos denominados eixo real e eixo imaginário conforme mostra a Figura 1.
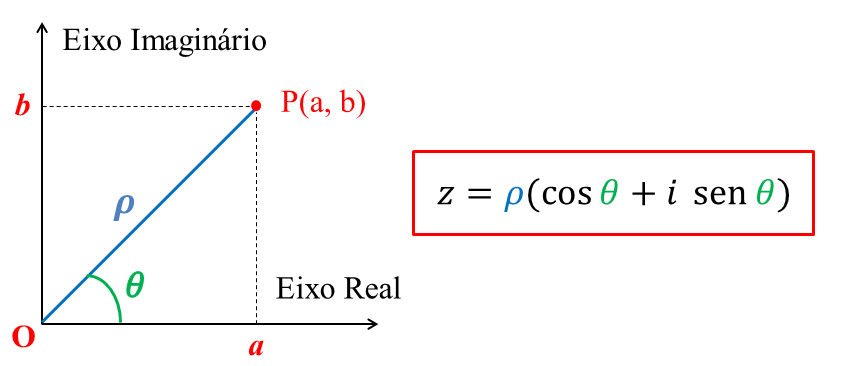
O ponto P(a, b), afixo do número complexo z = a + bi, pode ser localizada por meio das coordenadas polares p (rô) e 0 (teta). O número p (rô), chamado módulo do número complexo z, pode também ser indicado por |z|. Geometricamente, representa a distância do ponto P à origem do sistema cartesiano sendo calculado por meio da fórmula apresentada na Figura 2.
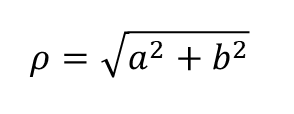
O número 0 (teta) denomina-se argumento do número complexo z. É o ângulo formado pelo segmento OP com o eixo real. Com 0 < 0 < 2pi ou 0 < 0 < 360° chamaremos argumento principal. Sendo calculado por meio da fórmula mostrada na Figura 3.
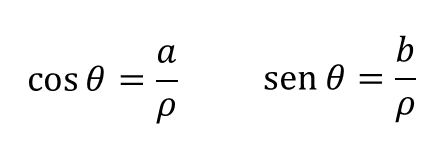
Exercícios Resolvidos
Escreva os seguintes números complexos na forma trigonométrica:
a) z = -5V3/2 + 5/2i
b) z = 2i
c) z = 1 – iV3
Obtenha a forma algébrica de cada um dos seguintes números complexos:
a) z = 4(cos 120° + i sen 120°)
b) z = 6(cos 4pi/3 + i sen 4pi/3)
c) z = 3(cos 90° + i sen 90°)
d) z = cos 3pi/2 + i sen 3pi/2
e) z = cos 210° + i sen 210°
