Função Quadrática

---

Chama-se função quadrática, ou função polinomial do 2º grau, qualquer função f de R em R dada por uma lei da forma f(x) = ax² + bx + c, em que a, b e c são números reais e a diferente de 0.

Exemplos:
f(x) = 2x² + 3x + 5; logo: a = 2, b = 3 e c = 5
f(x) = x² + 4x – 4; logo: a = 1, b = 4 e c = -4.

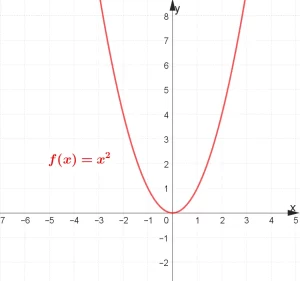
Se a expressão da função tiver coeficientes a = 1, b = 0 e c = 0. Ou seja, f(x) = x², o gráfico da função será uma parábola conforme mostrado na Figura 1.