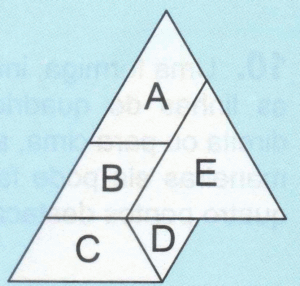
Questão 1 – Cinco cartões iguais A, B, C, D e E, em forma de triângulo equilátero, foram colados em uma cartolina, um por vez. A figura mostra como ficaram esses cartões. Qual foi o terceiro cartão colado?
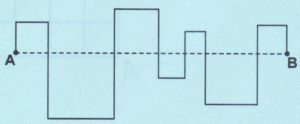
Questão 2 – Ao passear pela cidade, em vez de pegar uma avenida em linha reta que liga os pontos A e B, João caminhou pelos quarteirões quadrados da cidade, conforme indicado na figura, percorrendo um total de 6 km. Qual é a distância, em linha reta, entre os pontos A e B?
Questão 3 – João tem bolas e caixas numeradas. Ele colocou as bolas 1 e 2 na primeira caixa, as de números 3, 4 e 5 na segunda caixa, as de números 6 e 7 na terceira caixa, as de números 8, 9 e 10 na quarta caixa, e assim por diante, ora colocando duas, ora colocando três bolas em caixas consecutivas. Qual é a caixa na qual João colocou a bola de número 2023?
Questão 4 – Qual é o valor da expressão 20235 x 20235 – 20238 x 20232?
Questão 5 – Um carro viaja de pirajuba a Quixajuba com velocidade constante de 60 km/h, em uma estrada que passa por Arraial. Às 11 horas, o carro havia percorrido 1/4 da distância entre Pirajuba e Arraial e, ás 15 horas, havia percorrido 3/4 da distância entre Arraial e Quixajuba. Qual é a distância entre Pirajuba e Quixajuba?
Questão 6 – Seja x um número tal que x² – 3x + 1 = 0. Qual é o valor de x² + 1/x²?
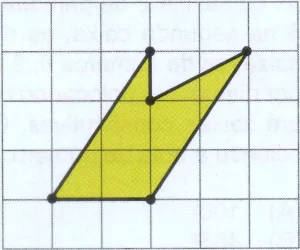
Questão 7 – A área do polígono amarelo com vértices em pontos do quadriculado é 30 cm². Qual é a área, em cm², de cada quadradinho do quadriculado?
Questão 8 – Miguel formou uma lista de oito números, obtidos preenchendo os espaços da expressão abaixo com todas as combinações possíveis de sinais + e -. _ 1 _ V2 _ V3
Qual é o produto desses oito números?
Questão 9 – As idades de três crianças são 7, 8 e 9 anos. Na figura, vemos a resposta de cada uma delas, quando perguntadas sobre suas idades. A criança com 8 anos foi a única que mentiu.
A criança mais velha e a criança mais nova são, nessa ordem,

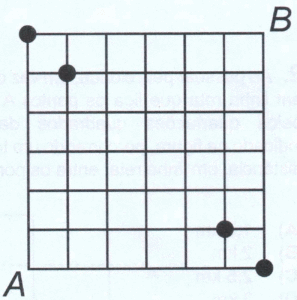
Questão 10 – Uma formiga, inicialmente no vértice A, anda sobre as linhas do quadriculado da figura, sempre para a direita ou para cima, até chegar ao vértice B. De quantas maneiras ela pode fazer isso passando por algum dos quatro pontos destacados?
Questão 11 – Os atletas André, Bruno e Carlos correm sempre a uma velocidade constante. Em uma corrida de 100 metros, André deu a Bruno uma vantagem de 20 metros e eles chegaram juntos. Em uma corrida de 400 metros, Bruno deu a Carlos uma vantagem de 20 metros e eles chegaram juntos. Quantos metros de vantagem André deve dar a Carlos para que eles cheguem juntos em uma corrida de 800 metros?

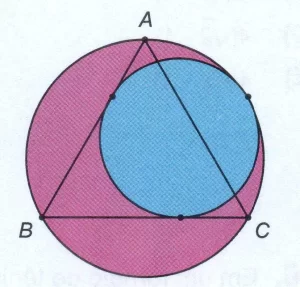
Questão 12 – Na figura, ABC é um triângulo equilátero e a circunferência menor é tangente a dois lados do triângulo e ao círculo maior, como indicado. A região rosa é a que está dentro do círculo maior e fora do círculo menor.
Qual é a razão entre as áreas destacadas em azul e rosa?
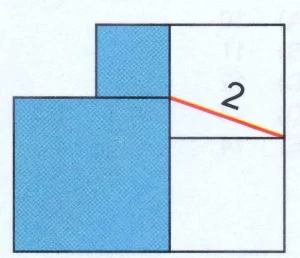
Questão 13 – A figura a seguir é formada por quatro quadrados. A medida do segmento destacado em vermelho é 2. Qual é a soma das áreas dos quadrados azuis?
Questão 14 – Qual é a quantidade máxima de números distintos de dois algarismos que se pode escrever sem que a soma de quaisquer dois deles seja igual a 86?
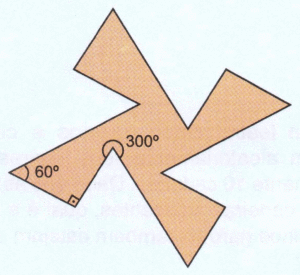
Questão 15 – A figura tem 8 lados de medida de 10 cm, 4 lados de medida 20 cm, 4 ângulos de 60°, 4 ângulos de 90° e 4 ângulos de 300°. Qual é a área da figura?
Questão 16 – Considere o conjunto dos primeiros 17 inteiros positivos, {1, 2, 3, …, 17}. Dois números desse conjunto são escolhidos de forma que o produto desses dois números seja igual à soma dos 15 números restantes. Qual é o valor desse produto?
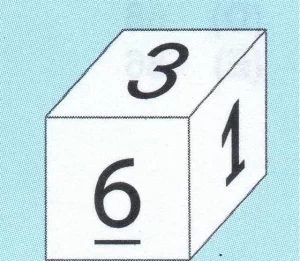
Questão 17 – Nas faces de um cubo estão escritos números inteiros positivos diferentes, entre os quais 1, 3 e 6, como na figura. O produto de números escritos em faces opostas é sempre o mesmo. Além disso, existem 3 faces diferentes nas quais os números escritos têm produto igual a 98. Qual é o maior número que aparece em alguma face desse cubo?
Questão 18 – Em um teatro, cinco garotos e cinco garotas escolheram aleatoriamente seus lugares em uma fila com exatamente 10 cadeiras. Dado que as cinco garotas estão em 5 cadeiras adjacentes, qual é a probabilidade de que os cinco garotos também estejam em 5 cadeiras adjacentes?

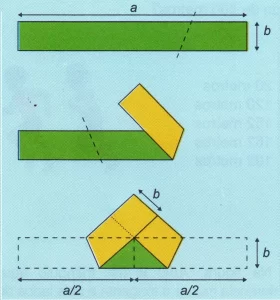
Questão 19 – Uma tira retangular tem comprimento a e largura b. Ao dobrar a tira, a sobreposição de suas pontas formou um quadrado de lado b e o resultado da dobra foi um pentágono sem nenhum buraco no centro, como indicado nas figuras. Qual a razão a/b?
Questão 20 – Em um torneio de tênis, cada jogador foi escalado para jogar contra cada um dos outros jogadores uma única vez. Entretanto, durante o evento, três jogadores desistiram do torneio. Sabemos que cada um dos desistentes jogou duas partidas. Se o torneio teve exatamente 50 jogos, quantos jogadores começaram o torneio?


