OBMEP 2024 – Nível 3

Questão 1
A figura mostra a localização de dois números x e y na reta numérica. Qual alternativa apresenta o menor número?
(A) x + y
(B) xy
(C) x/y
(D) x
(E) x²

Questão 2
No quadriculado, a soma dos elementos de cada linha e de cada coluna são iguais. Qual é o valor de a + b – c?
(A) 6
(B) 7
(C) 8
(D) 9
(E) 10

Questão 3
Na figura, ABCD e BEFC são quadrados, cada um com 60 cm² de área. Qual é a área, em cm², da região cinza?
(A) 30
(B) 70
(C) 100
(D) 45
(E) 60

Questão 4
Um celular tem espaço para gravar 3 horas de vídeo em qualidade normal ou 2 horas em alta qualidade. Se já foram gravadas 2 horas de vídeo em qualidade normal, qual é o tempo que resta para gravar vídeos em alta qualidade?
(A) 40 minutos
(B) 120 minutos
(C) 60 minutos
(D) 30 minutos
(E) 90 minutos

Questão 5
Na sequência de figuras formadas por triângulos equiláteros idênticos, mostrada abaixo, cada figura é formada pela figura anterior acrescida da menor quantidade possível de triângulos que escondem o perímetro da figura anterior. Quantos triângulos devem ser adicionados à Figura 9 para se obter a Figura 10?
(A) 21
(B) 30
(C) 27
(D) 18
(E) 24

Questão 6
Vinte e quatro retas são desenhadas no plano de modo que cada reta seja paralela a exatamente outras três. Além disso, não há três retas que se cruzem em um mesmo ponto. Qual é o número total de pontos de interseção entre essas retas?
(A) 120
(B) 200
(C) 240
(D) 169
(E) 276

Questão 7
Os 45 alunos de uma turma compraram os 100 bilhetes de um sorteio, em diferentes quantidades, de acordo com a tabela. É mais provável que o bilhete sorteado tenha sido comprado por um aluno que comprou 1, 2, 3, 4 ou 5 bilhetes?
(A) 2 bilhetes
(B) 4 bilhetes
(C) 3 bilhetes
(D) 1 bilhete
(E) 5 bilhetes

Questão 8
Um mágico tem quatro coelhos de cores diferentes e quatro cartolas numeradas de 1 a 4. De quantas maneiras distintas dois coelhos podem ficar em uma mesma cartola e os outros dois em outra?
(A) 72
(B) 36
(C) 16
(D) 4
(E) 360

Questão 9
O desenho a seguir representa um mapa que tem 7 cidades, representadas por pontos, e 5 estradas, representadas por curvas. Qual é o menor número de estradas que devem ser incluídas no desenho para que de cada cidade parta o mesmo número de estradas?
(A) 5
(B) 4
(C) 10
(D) 11
(E) 9

Questão 10
Pascoal colocou os números 5, 6, 7, 8 e 9 nas casas do tabuleiro abaixo, um número em cada casa, sem repetir números nas linhas e nas colunas. Em seguida, ele somou os oito números colocados na primeira e na última colunas. Qual dos números abaixo não pode ser um resultado para a soma que Pascoal fez?
(A) 53
(B) 57
(C) 58
(D) 55
(E) 52

Questão 11
Considere um hexágono regular de área 1 e todos os triângulos cujos vértices são também do hexágono. Qual é a soma das áreas de todos esses triângulos?
(A) 7
(B) 5
(C) 4
(D) 3
(E) 6

Questão 12
Uma folha quadrada de papel, branca de um lado e cinza do outro, tem área igual a 75 cm². A folha é dobrada de modo que o vértice P seja levado a um ponto P’ da diagonal PR, conforme a figura. Depois da dobra, as partes branca e cinza visíveis ficaram com a mesma área. Qual é a distância, em centímetros, do ponto P’ até o ponto P?
(A) 6,0
(B) 7,5
(C) 5,0
(D) 10,0
(E) 7,0

Questão 13
Em um conjunto de números inteiros positivos, a média aritmética dos dois números é 50, dos três maiores é 48, dos quatro maiores é 46 e assim por diante, diminuindo de 2 em 2. Qual é o menor número que pode pertencer a esse conjunto?
(A) 1
(B) 5
(C) 4
(D) 3
(E) 2

Questão 14
O triângulo ABC da figura é isósceles e sua base AB mede 8 cm. Os pontos M e N são pontos médios dos lados AC e BC, respectivamente. Qual é o perímetro, em centímetros, do triângulo ABC?
(A) 30
(B) 38
(C) 34
(D) 36
(E) 32

Questão 15
Alexandra comprou o ingresso com número de assento 100 em um teatro com assentos numerados de 1 a 120. A figura mostra a numeração de alguns assentos, com poltronas pares de um lado e ímpares do outro, em ordem crescente a partir do corredor. Os demais assentos seguem o mesmo padrão de numeração. Pedro quer sentar o mais próximo possível de Alexandra e só restam os ingressos para os assentos 94, 99, 101, 102 e 112. Qual é o número do assento que Pedro deve comprar?
(A) 102
(B) 99
(C) 112
(D) 94
(E) 101

Questão 16
Ana, Bia e Carla visitaram a floricultura de seu bairro. O vendedor separou as 5 flores mostradas na figura e disse que iria presentear cada uma com uma dessas flores.
Carla escutou a seguinte conversa entre Bia e Ana:
Bia disse: “Oi Ana, eu e Carla sabemos a cor de cada uma das flores que vamos ganhar, mas nem eu nem ela sabemos as quantidades de pétalas das flores que cada uma de nós irá ganhar”.
Ana disse: “Eu sei a quantidade de pétalas da flor que vou ganhar, mas não sei a cor”.
A partir dessa conversa, Carla descobriu a flor que Ana vai ganhar. Qual é essa flor?

Questão 17
Oito pessoas, incluindo os irmãos, Alexandre, Bruno e Carlito, vão passear em 4 canoas diferentes. Em cada canoa vão sentar 2 pessoas. As 8 pessoas são distribuídas aleatoriamente entre as 4 canoas. Qual é a probabilidade de que dois irmãos quaisquer não fiquem juntos em uma mesma canoa?
(A) 2/7
(B) 1/9
(C) 2/4
(D) 6/8
(E) 4/7

Questão 18
Joãozinho tem três dados com faces numeradas de 1 a 6. Nesses dados, a soma dos números em faces opostas é sempre 7. Ele empilhou os dados de tal forma que os números em cada par de faces em contato somam 5 e o número 1 ficou visível, como indicado na figura. Qual é o número que ficou na face superior da pilha?
(A) 4
(B) 3
(C) 6
(D) 2
(E) 5

Questão 19
As figuras mostram as vistas de frente, de cima e da esquerda de um sólido montado com cubo iguais. Quantos cubos tem esse sólido?
(A) 14
(B) 13
(C) 15
(D) 12
(E) 16

Questão 20
Uma competição de matemática consiste de uma prova com três problemas. Cada aluno pode obter nota 0, 1 ou 2 em cada problema. Após a correção das provas, constatou-se que não existiam dois alunos com notas iguais nos mesmos dois problemas. Qual é o número máximo de alunos que podem ter participado da competição?
(A) 12
(B) 6
(C) 16
(D) 9
(E) 8

Questão 1

Ana e Pedro cortam pedaços de papel que estão em uma cesta.
● Sempre que Ana pega um pedaço, corta em cinco pedaços e devolve todos eles para a cesta.
● Sempre que Pedro pega um pedaço, corta em três pedaço e devolve todos eles para a cesta.
Inicialmente há três pedaços de papel na cesta.

a) Quantos pedaços de papel ficarão na cesta depois de Ana e Pedro pegarem um pedaço cada um e devolverem os pedaços cortados para a cesta?
b) Descreva uma maneira de Ana e Pedro pegarem, cortarem e devolverem todos os pedaços de papel da cesta para que, a partir dos três pedaços iniciais, a cesta fique com 11 pedaços.
c) Explique por que, a partir dos três pedaços iniciais, a cesta nunca ficará com 2024 pedaços após Ana e
Pedro devolverem todos os pedaços cortados para a cesta.

Questão 2

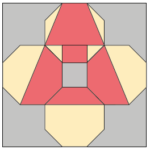
Quatro octógonos regulares de lados medindo 1 cm foram desenhados em um cartão quadrado, como na figura. Cada octógono tem um lado na borda do cartão e octógonos adjacentes têm um lado em comum.
a) Qual é a área do cartão?
b) Qual é a área da região cinza?

c) Qual é a área da parte pintada em vermelho sobre os octógonos?

Questão 3

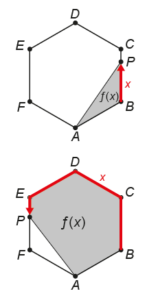
Um hexágono regular ABCDEF tem lados de medida 1. Um ponto P desloca-se na borda do hexágono, a partir do vértice B, passando pelos vértices C, D e E até chegar ao vértice F. Seja x a distância percorrida pelo ponto P e seja ƒ(x) a área da região com vértices em P, A e outros vértices do hexágono pelos quais P já passou. A figura mostra algumas dessas regiões.
a) Calcule f(1)
b) Determine a expressão f(x) quando P se desloca no lado DE.
c) Esboce o gráfico de f.

Questão 4

Um terreno quadrado foi dividido em 9 lotes também quadrados, cercados por muros. Câmeras instaladas no encontro de dois ou mais muros vigiam os muros adjacentes ao ponto de instalação. Na figura temos duas câmeras vigiando 6 muros.
a) Indique uma posição de duas câmeras na figura abaixo de modo que elas vigiem a maior quantidade possível de muros.
b) Qual é o número mínimo de câmeras necessárias para vigiar os 12 muros na fronteira do terreno? Justifique sua resposta.
c) Encontre o número mínimo de câmeras necessárias para vigiar todos os muros do terreno. Justifique sua resposta.

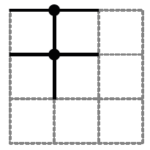
Questão 5

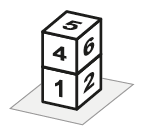
Marina tem vários dados idênticos com faces numeradas de 1 a 6. Nesses dados, a soma dos números em faces opostas é sempre igual a 7. Ela junta ou empilha alguns desses dados sobre uma mesa e anota a soma de todos os números que consegue ver ao dar uma volta ao redor da mesa. Por exemplo, para os dados a figura ao lado ela anotou o número 33.

a) Qual é o número que Marina deve anotar para os dados da figura abaixo?

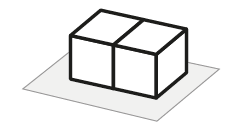
b) Qual é o menor número possível que Marina pode anotar para dois dados juntos sobre a mesa, como indicado na figura abaixo?

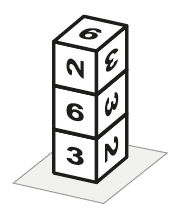
c) Marina anotou o número 88 para uma pilha de dados como indicado na figura abaixo. Quais números podem ficar no topo dessa pilha? Justifique sua resposta.

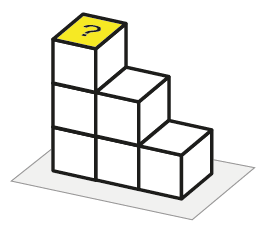
Questão 6

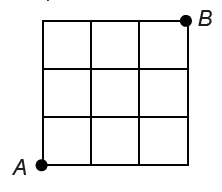
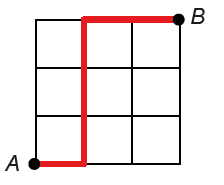
Duas formigas caminham sobre as linhas do quadriculado da figura. No mesmo instante, uma parte do ponto A e a outra, do ponto B. A velocidade da formiga que parte de B é dois terços da velocidade da formiga que parte de A. A formiga que parte de A sempre caminha para a direita ou para cima, e a formiga que parte de B sempre caminha para a esquerda ou para baixo. Cada vez que uma delas têm duas direções para prosseguir, essas direções têm probabilidade 1/2 de ser escolhida. Por exemplo, a probabilidade de que a formiga que parte de A siga o caminho indicado na figura é (1/2) × (1/2) × (1/2) × (1/2) = 1/16, pois ela tem que fazer 4 escolhas de direções.

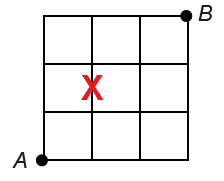
a) Qual é a probabilidade de que a formiga que parte de A passe pelo lado do quadriculado marcado com X?

b) Marque abaixo, com um X, os lados do quadriculado onde as formigas podem se encontrar.
c) Qual é a probabilidade de que as formigas se encontrem?