Introdução
Muitas situações em Matemática utilizam regras precisas, como por exemplo, equações e funções. Porém, em muitas outras situações existem incertezas. Como podemos modelar essas situações? Existem padrões matemáticos nessas situações? Existe confiabilidade nesses padrões? O conceito de probabilidade ajuda a responder essas questões.
Utilizando como exemplo a jogada de um dado onde se espera como resultado a face igual a 3. Obviamente é impossível prever qual face será mostrada. Porém, a ideia principal é se o dado for jogado uma infinidade de vezes, a face 3 será mostrada em um sexto de vezes da quantidade de jogadas. Isso acontece porque a chance de sair cada uma das seis faces (1, 2, 3, 4, 5 e 6) são igualmente prováveis. Logo, devemos dizer que a probabilidade de sair a face 3 é igual a um sexto (1/6).
Outro exemplo utilizando um baralho de 52 cartas. Ao retirar uma carta do baralho, quais são as chances de sair um ás? Considerando que cada carta tem igual chance de sair e sabendo que um baralho tem quatro ases, a probabilidade de se tirar um ás é 4/52.
Exemplos como os citados aparecem em muitas situações do dia-a-dia. Por exemplo, uma organização social deve escolher cinco pessoas, entre seus cinquenta integrantes, para compor uma comissão. A escolha será feita de forma aleatória. Quais são as chances da comissão ser composta somente por mulheres?
Atualmente, probabilidade é uma ferramenta indispensável para tomada de decisão em negócios, indústria e pesquisas científicas. Por exemplo, para determinar a efetividade de novos remédios e pesquisas eleitorais.
Definição
Suponha que entre as cidades de Aracaju, Brasília e Cuiabá existam dois modos (avião e ônibus) de uma pessoa viajar de Aracaju para Brasília, e três modos (avião, ônibus e carro) para viajar de Brasília para Cuiabá. De quantos modos distintos é possível utilizar os meios de transporte disponíveis para sair de Aracaju e chegar a Cuiabá passando por Brasília?
A resposta para essa pergunta é dividir o problema em partes menores. Na primeira parte, de Aracaju para Brasília existem duas escolhas (avião e ônibus) e na segunda parte, de Brasília para Cuiabá existem três escolhas ( avião, ônibus e carro). Logo, o número de rotas distintas é 2 . 3 = 6.
A Figura 1 mostra a situação descrita acima.
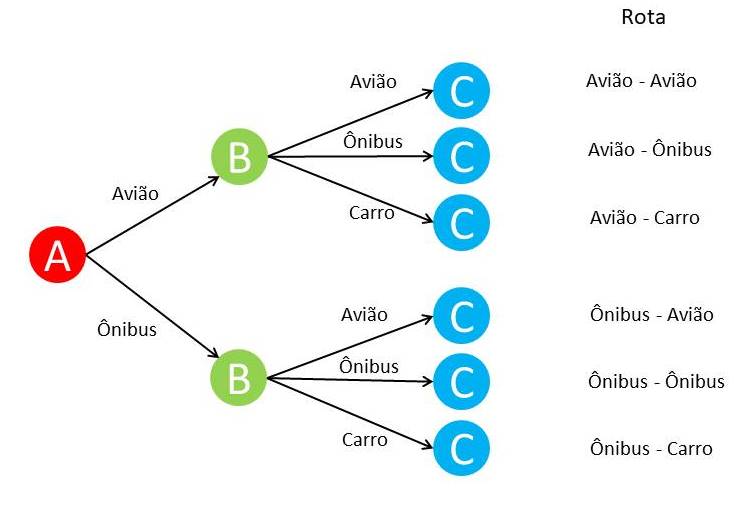
Desse modo, podemos enunciar o Princípio Fundamental da Contagem (PFC).
Se dois eventos ocorrem em sequência, e o primeiro evento pode ocorrer de m modos distintos e o segundo evento pode ocorrer de n modos distintos. Então, os dois eventos pode ocorrer em sequência de m . n modos distintos.
Exemplo
Uma lanchonete oferece três tipos de sanduíche e oito tipos de sucos. De quantos modos distintos é possível comprar um lanche composto por um sanduíche e um suco?
Solução: Existem dois passos para se escolher o lanche. No primeiro passo, três escolhas de sanduíche. No segundo passo, oito escolhas de suco. Podemos pensar os passos como espaço a serem preenchidos conforme mostra a Figura 2.
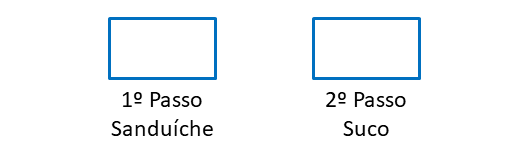
Portanto, no primeiro espaço preenchemos com o número 3 e o segundo espaço preenchemos com 8. Multiplicamos 3 por 8, o resultado será 24, conforme Figura 3.
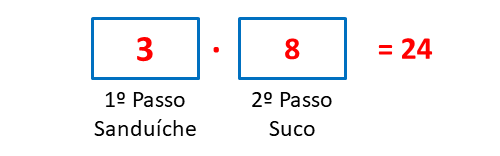
Exercícios Resolvidos
Considerando os algarismos 1, 2, 3, 4, 5, 6, 7 e 8, responda:
a) Quantos números de quatro algarismos podemos formar?
b) Quantos números pares de quatro algarismos podemos formar?
c) Em relação ao total do item a, qual é a porcentagem correspondente aos números que têm todos os algarismos distintos?
Responda:
a) Uma moeda é lançada duas vezes sucessivamente. Quantas sequências de faces podem ser obtidas? Quais são elas?
b) Quantas sequências de faces poderiam ser obtidas, caso a moeda fosse lançada quatro vezes sucessivamente? E cinco vezes? E dez vezes?
c) Uma moeda foi lançada n vezes sucessivamente. Sabendo que o número de sequências de faces que poderiam ter sido obtidas é 419, qual é o valor de n?
Em um teste vocacional, um jovem deve responder a doze questões, assinalando, em cada uma, uma única alternativa, escolhida entre “sim”, “não” e “às vezes”. De quantas formas distintas o teste poderá ser respondido?
Para ir à praia, Sílvia pretende colocar um maiô e uma canga. Sabendo que ela possui cinco maiôs diferentes e três modelos diferentes de canga, determine o número de maneiras distintas de Sílvia se vestir.
Um restaurante oferece almoço a R$ 40,00, incluindo: entrada, prato principal e sobremesa. De quantas formas distintas um cliente pode fazer seu pedido, se existem quatro opções de entrada, três de prato principal e duas de sobremesa?
Responda:
a) Quantos números de cinco algarismos existem?
b) Quantos números ímpares de cinco algarismos existem?
c) Quantos números de cinco algarismos são maiores que 71265?
d) Quantos números de cinco algarismos distintos começam por 7?
Três amigos chegam um pouco atrasados para uma aula de bicicleta na academia e encontram cinco bicicletas vagas. De quantos modos distintos eles podem se distribuir nas bicicletas vagas?
