Probabilidade
O termo probabilidade se refere ao estudo da aleatoriedade e da incerteza. O estudo da probabilidade como ramo da matemática data de mais de 300 anos e o interesse por seu estudo esteve relacionada a questões que envolviam jogos de azar.
Os primeiros registros ligados à teoria da probabilidade aparecem na obra do italiano Girolamo Cardano (1501-1576) sobre jogos de azar. Cerca de cem anos depois, Blaise Pascal deu novo impulso ao desenvolvimento da teoria da probabilidade, por meio das cartas que trocou com Pierre de Fermat (1601-1665). As cartas continham questões propostas por um apostador, Chevalier de Meré, que estava interessado na distribuição igualitária das chances de vencer entre os jogadores quando o jogo é interrompido. Em sua obra sobre o triângulo aritmético, datada de 1654, há também alguns tópicos sobre probabilidade.
No entanto, o primeiro artigo completo sobre o assunto só foi escrito em 1713, por Jacques Bernoulli, na obra Ars Conjectandi (Arte de conjecturar), que continha, inclusive, uma detalhada exposição sobre permutações e combinações. A partir de então, outros matemáticos dariam valiosas contribuições para o desenvolvimento da teoria das probabilidades, cujas aplicações em áreas como Biologia, Economia, Saúde, tábuas atuariais etc. não tardariam a ser reconhecidas.
A teoria da probabilidade está presente em nosso cotidiano, como por exemplo, nas loterias de números, Mega-Sena, Lotofácil, e outras. Muitas vezes usada de maneira informal para expressar alguma incerteza ou chance de ocorrer determinada situação. Por exemplo, quando os telejornais informam a previsão do tempo.
Definição de Probabilidade
Considere o espaço amostral S de um experimento aleatório em qual os resultados são igualmente prováveis. Então, a probabilidade P(E) de ocorrer o evento E é a razão entre o número de elementos do evento n(E) e o número de elementos do espaço amostral n(S).
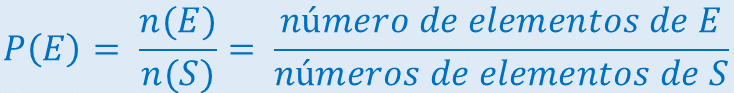
Exemplo
Uma moeda é lançada três vezes e os resultados são anotados. Qual é a probabilidade de sair exatamente duas caras?
Solução: Sendo C = cara e K = Coroa, o espaço amostral terá o seguinte conjunto de resultados. S = { CCC, CCK, CKC, CKK, KCC, KCK, KKC, KKK }, ou seja 8 elementos. Logo, n(S) = 8. O evento desejado será um subconjunto do espaço amostral. E = { CCK, CKC, KCC }. Logo, n(E) = 3. Portanto,
P(E) = n(E) / n(S) P(E) = 3 / 8
Exercícios Resolvidos de Probabilidade
Uma urna contém 100 bolas de mesma massa e mesmo tamanho numeradas de 1 a 100. Uma delas é extraída ao acaso. Qual a probabilidade de o número sorteado ser:
a) 18?
b) 57?
c) maior que 63?
d) formado por dois algarismos?
e) um quadrado perfeito?
Uma caixa contém 10 tiras de cartolina, todas do mesmo tamanho e textura. Em cada tira está escrita uma única letra do conjunto cujos elementos são as vogais e as cinco primeiras consoantes do alfabeto. Não existem tiras com a mesma letra. Uma tira é sorteada ao acaso. Qual é a probabilidade de que a letra escrita na tira sorteada seja:
a) E?
b) C?
c) J?
d) consoante?
Ao lançarmos um dado duas vezes sucessivamente, qual é a probabilidade de que:
a) o número 1 ocorra em ao menos um lançamento?
b) a soma dos pontos obtidos seja 7?
c) os números obtidos sejam diferentes entre si?
d) o módulo da diferença entre os pontos obtidos seja maior que 2?
De um baralho de 52 cartas, uma é extraída ao acaso. Qual é a probabilidade de que a carta sorteada:
a) seja o sete de copas?
b) seja de ouros?
c) não seja o valete de espadas?
d) não seja de ouros nem de copas?

