Introdução
Por meio da tabela verdade representamos as operações lógicas envolvendo os conectivos. As frases das sentenças proposicionais são convertidas em letras, p, q, r… para facilitar a escrita e combinadas com os conectivos.
Conectivo Não
Uma proposição p ou é verdadeira ou é falsa, não havendo outra possibilidade. Logo, quando p é verdadeira (V), a sua negação, representada por ~p, é falsa. Do mesmo modo, quando p é falsa (F), a sua negação é verdadeira. A Figura 1 resume este parágrafo.
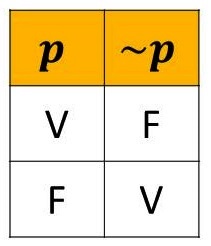
Exemplos:
p: Lima é capital do Peru (p = V), Negação: Lima não é capital do Peru.
p: Santiago não é capital do Chile (p = F), Negação: Santiago é capital do Chile.
Conectivo E
Quando duas proposições simples são ligadas pela palavra E, a proposição composta resultante é denominada conjunção. Sendo p (antecedente), a primeira proposição e q (consequente) a segunda proposição, a conjunção das duas é representada por p ^ q.
A conjunção tem valor lógico Verdade quando ambas as proposições são verdadeiras e Falso nos demais casos. A Figura 2 ilustra o citado.
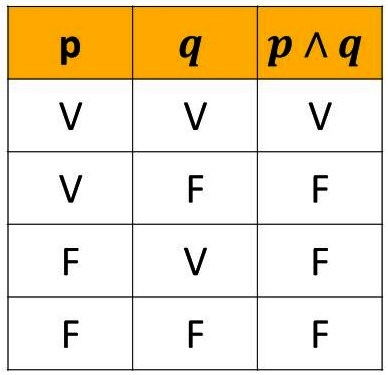
Exemplo:
p: Brasília é capital do Brasil. (V)
q: 17 é número primo. (V)
p ^ q = Brasília é capital do Brasil (V) e 17 é um número primo (V) = V
Conectivo OU
Quando duas proposições simples são ligadas pela palavra OU, a proposição composta resultante é denominada disjunção. Sendo p (antecedente), a primeira proposição e q (consequente) a segunda proposição, a disjunção das duas é representada por p V q.
Observe que linguagem cotidiana utilizamos a palavra OU em dois sentidos. No sentido exclusivo ( Carlos é Baiano ou Gaúcho) onde uma opção exclui a outra. Ou no sentido inclusivo (Carlos é Professor ou Médico), Carlos pode ter somente uma profissão ou as duas. O conectivo OU utiliza o sentido inclusivo. A Figura 3 ilustra o citado.
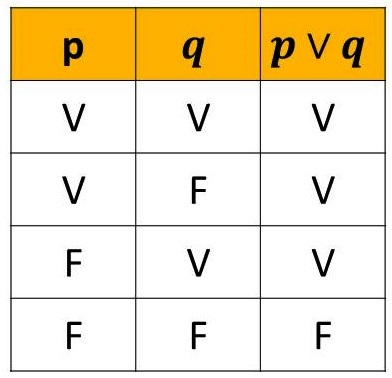
Exemplo:
p: O cobre é um metal. (V)
q: O plástico é um metal. (F)
p v q = O cobre é um metal (V) ou O plástico é um metal (F) = V
Conectivo SE … ENTÃO
Quando duas proposições simples são ligadas pelas palavras SE … ENTÃO, a proposição composta resultante é denominada condicional. Sendo p (antecedente), a primeira proposição e q (consequente) a segunda proposição, a condicional das duas é representada por p > q.
A proposição condicional tem valor lógico Falso quando o antecedente é verdadeiro e o consequente é falso e valor lógico Verdade para os demais casos. A Figura 4 mostra sua tabela verdade.
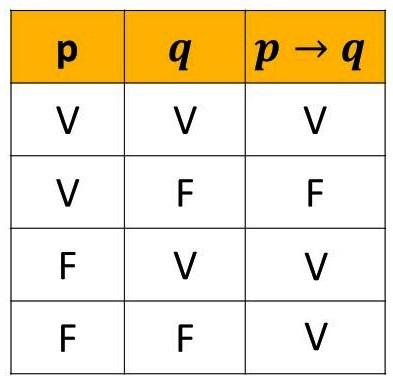
Exemplo:
p: 5 + 4 = 9. (V)
q: O Nilo é um rio europeu. (F)
p > q: Se 5 + 4 = 9 (V), então o Nilo é um rio Europeu (F) = F
Conectivo SE e SOMENTE SE
Quando duas proposições simples são ligadas pelas palavras SE e SOMENTE SE, a proposição composta resultante é denominada bicondicional. Sendo p (antecedente), a primeira proposição e q (consequente) a segunda proposição, a bicondicional das duas é representada por p <> q.
A proposição bicondicional é Verdade quando antecedente e consequente tem valores lógicos iguais e Falso quando tem valores lógicos diferentes conforme mostra a Figura 5.
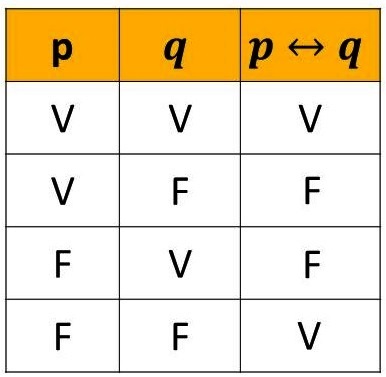
Exemplo:
p: Brasília é capital da Argentina (F)
q: Um número par é divisível por 2. (V)
p <> q: Brasília é capital da Argentina (F) se e somente se um número par é divisível por 2 (F) = F
Questões de Concursos
Na proposição “André é analista de sistema e Raul é engenheiro”, o conectivo lógico utilizado denomina-se:
a) Condicional
b) Bicondicional
c) Disjunção
d) Conjunção
Bibliografia:
ALENCAR FILHO, Edgard, Iniciação a Lógica Matemática. São Paulo: Nobel, 2002.
KELLER, Vicente; BASTOS, Cleverson Leite, Aprendendo Lógica. Petrópolis: Vozes, 2002.
MACHADO, Nilton José, Matemática por Assunto. São Paulo: Scipione, 1988.
NETO, Aref Antar; et al, Noções de Matemática. São Paulo: Moderna, 1982.

